what is the greatest possible number of solutions to the following system of equations? 1 2 3 4
Systems of Equations and Inequalities
Systems of Linear Equations: Ii Variables
Learning Objectives
In this department, y'all volition:
- Solve systems of equations by graphing.
- Solve systems of equations past commutation.
- Solve systems of equations by improver.
- Identify inconsistent systems of equations containing ii variables.
- Limited the solution of a organisation of dependent equations containing two variables.

A skateboard manufacturer introduces a new line of boards. The manufacturer tracks its costs, which is the amount it spends to produce the boards, and its revenue, which is the amount it earns through sales of its boards. How tin can the company determine if it is making a profit with its new line? How many skateboards must exist produced and sold earlier a profit is possible? In this section, we will consider linear equations with two variables to answer these and similar questions.
Introduction to Systems of Equations
In order to investigate situations such as that of the skateboard manufacturer, we need to recognize that we are dealing with more than 1 variable and likely more than one equation. A organisation of linear equations consists of ii or more linear equations fabricated up of two or more variables such that all equations in the arrangement are considered simultaneously. To find the unique solution to a system of linear equations, we must detect a numerical value for each variable in the system that volition satisfy all equations in the organization at the same time. Some linear systems may not have a solution and others may take an space number of solutions. In order for a linear organization to have a unique solution, there must be at to the lowest degree as many equations every bit there are variables. Even so, this does non guarantee a unique solution.
In this section, we will look at systems of linear equations in two variables, which consist of ii equations that contain 2 different variables. For example, consider the following arrangement of linear equations in ii variables.
![]()
The solution to a system of linear equations in two variables is any ordered pair that satisfies each equation independently. In this example, the ordered pair (4, 7) is the solution to the system of linear equations. We can verify the solution by substituting the values into each equation to see if the ordered pair satisfies both equations. Soon we volition investigate methods of finding such a solution if it exists.
![]()
In addition to considering the number of equations and variables, we can categorize systems of linear equations past the number of solutions. A consistent organisation of equations has at least one solution. A consequent system is considered to exist an contained system if information technology has a single solution, such as the example nosotros only explored. The two lines accept different slopes and intersect at one point in the plane. A consequent system is considered to be a dependent organization if the equations take the same gradient and the aforementioned y-intercepts. In other words, the lines coincide so the equations stand for the aforementioned line. Every signal on the line represents a coordinate pair that satisfies the organization. Thus, there are an infinite number of solutions.
Some other type of system of linear equations is an inconsistent system, which is one in which the equations represent ii parallel lines. The lines take the same slope and unlike y-intercepts. There are no points common to both lines; hence, there is no solution to the arrangement.
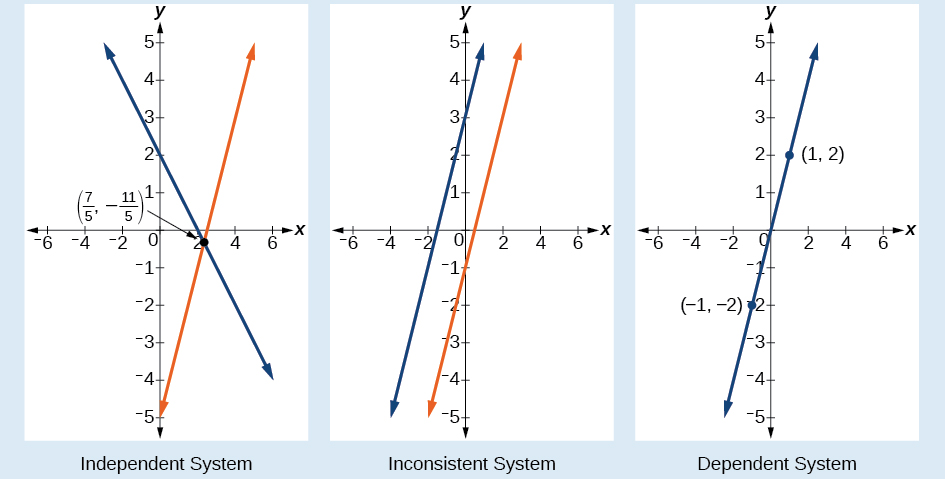
Types of Linear Systems
In that location are 3 types of systems of linear equations in two variables, and three types of solutions.
- An independent organisation has exactly 1 solution pair
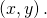 The point where the two lines intersect is the only solution.
The point where the two lines intersect is the only solution. - An inconsistent system has no solution. Notice that the two lines are parallel and volition never intersect.
- A dependent organization has infinitely many solutions. The lines are coincident. They are the same line, then every coordinate pair on the line is a solution to both equations.
(Figure) compares graphical representations of each type of arrangement.
How To
Given a system of linear equations and an ordered pair, determine whether the ordered pair is a solution.
- Substitute the ordered pair into each equation in the system.
- Determine whether true statements result from the substitution in both equations; if so, the ordered pair is a solution.
Determining Whether an Ordered Pair Is a Solution to a Arrangement of Equations
Determine whether the ordered pair![]() is a solution to the given organization of equations.
is a solution to the given organization of equations.
![]()
[reveal-answer q="fs-id1165135547124″]Show Solution[/reveal-reply]
[subconscious-answer a="fs-id1165135547124″]
Substitute the ordered pair![]() into both equations.
into both equations.
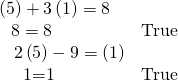
The ordered pair![]() satisfies both equations, so information technology is the solution to the organization.
satisfies both equations, so information technology is the solution to the organization.
[/subconscious-reply]
Assay
We can see the solution clearly by plotting the graph of each equation. Since the solution is an ordered pair that satisfies both equations, it is a point on both of the lines and thus the point of intersection of the ii lines. See (Effigy).
Try It
Decide whether the ordered pair![]() is a solution to the post-obit system.
is a solution to the post-obit system.
![]()
[reveal-respond q="fs-id1165135513561″]Show Solution[/reveal-reply]
[hidden-respond a="fs-id1165135513561″]
Not a solution.
[/hidden-respond]
Solving Systems of Equations past Graphing
There are multiple methods of solving systems of linear equations. For a organization of linear equations in two variables, we can determine both the blazon of organization and the solution past graphing the system of equations on the same set of axes.
Solving a System of Equations in Two Variables past Graphing
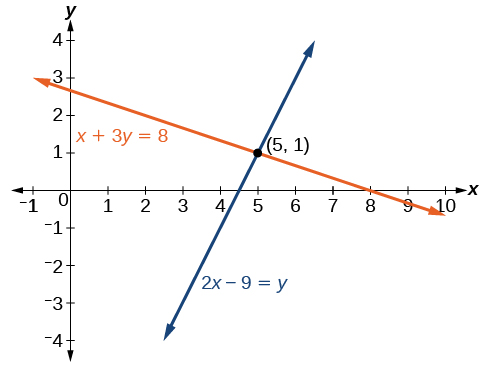
Solve the following arrangement of equations by graphing. Identify the type of system.
![]()
[reveal-answer q="970051″]Show Solution[/reveal-answer]
[hidden-respond a="970051″]
Solve the first equation for![]()
![]()
Solve the second equation for![]()
![]()
Graph both equations on the same fix of axes equally in (Figure).
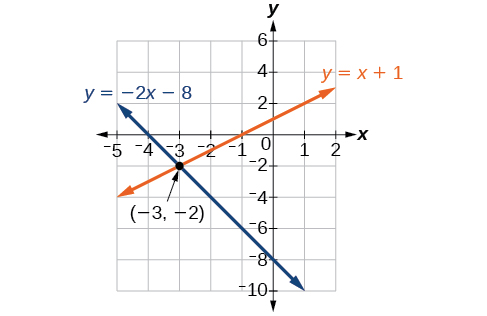
The lines appear to intersect at the bespeak![]() We can bank check to make sure that this is the solution to the arrangement by substituting the ordered pair into both equations.
We can bank check to make sure that this is the solution to the arrangement by substituting the ordered pair into both equations.
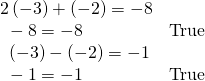
The solution to the arrangement is the ordered pair![]() and so the organisation is independent.
and so the organisation is independent.
[/subconscious-reply]
Try It
Solve the following arrangement of equations past graphing.
[reveal-answer q="192383″]Evidence Solution[/reveal-reply]
[hidden-answer a="192383″]
![]()
The solution to the system is the ordered pair![]()

[/hidden-reply]
Can graphing be used if the system is inconsistent or dependent?
Yes, in both cases nosotros tin still graph the arrangement to make up one's mind the type of arrangement and solution. If the two lines are parallel, the arrangement has no solution and is inconsistent. If the 2 lines are identical, the organisation has infinite solutions and is a dependent arrangement.
Solving Systems of Equations past Substitution
Solving a linear arrangement in two variables past graphing works well when the solution consists of integer values, merely if our solution contains decimals or fractions, it is not the most precise method. Nosotros will consider two more methods of solving a system of linear equations that are more than precise than graphing. One such method is solving a system of equations by the commutation method, in which we solve one of the equations for one variable and and so substitute the consequence into the 2d equation to solve for the 2nd variable. Think that nosotros tin can solve for just one variable at a time, which is the reason the substitution method is both valuable and practical.
How To
Given a organization of two equations in two variables, solve using the substitution method.
- Solve one of the two equations for one of the variables in terms of the other.
- Substitute the expression for this variable into the second equation, then solve for the remaining variable.
- Substitute that solution into either of the original equations to find the value of the kickoff variable. If possible, write the solution equally an ordered pair.
- Cheque the solution in both equations.
Solving a Arrangement of Equations in Two Variables by Commutation
Solve the post-obit organisation of equations by substitution.
![]()
[reveal-reply q="fs-id1165137849396″]Bear witness Solution[/reveal-reply]
[subconscious-answer a="fs-id1165137849396″]
First, we will solve the first equation for![]()
![]()
Now nosotros tin substitute the expression![]() for
for![]() in the second equation.
in the second equation.
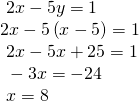
At present, nosotros substitute![]() into the first equation and solve for
into the first equation and solve for![]()
![]()
Our solution is![]()
Check the solution by substituting![]() into both equations.
into both equations.
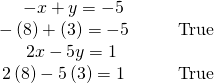 [/hidden-reply]
[/hidden-reply]
Effort It
Solve the following arrangement of equations past substitution.
![]()
[reveal-answer q="fs-id1165135516681″]Show Solution[/reveal-answer]
[subconscious-answer a="fs-id1165135516681″]
![]()
[/subconscious-answer]
Can the substitution method be used to solve whatever linear system in two variables?
Yes, but the method works best if one of the equations contains a coefficient of i or –1 so that nosotros do non accept to deal with fractions.
Solving Systems of Equations in Ii Variables past the Addition Method
A third method of solving systems of linear equations is the add-on method. In this method, nosotros add ii terms with the same variable, but contrary coefficients, and so that the sum is zero. Of form, non all systems are set up with the ii terms of ane variable having reverse coefficients. Often we must arrange one or both of the equations by multiplication and so that 1 variable will be eliminated by addition.
How To
Given a organization of equations, solve using the addition method.
- Write both equations with x– and y-variables on the left side of the equal sign and constants on the correct.
- Write one equation higher up the other, lining upwards respective variables. If ane of the variables in the top equation has the contrary coefficient of the aforementioned variable in the bottom equation, add the equations together, eliminating 1 variable. If not, use multiplication by a nonzero number and then that one of the variables in the top equation has the contrary coefficient of the same variable in the bottom equation, then add together the equations to eliminate the variable.
- Solve the resulting equation for the remaining variable.
- Substitute that value into i of the original equations and solve for the 2d variable.
- Check the solution by substituting the values into the other equation.
Solving a System by the Addition Method
Solve the given system of equations past addition.
![]()
[reveal-answer q="fs-id1165132078090″]Show Solution[/reveal-reply]
[hidden-respond a="fs-id1165132078090″]
Both equations are already set equal to a constant. Notice that the coefficient of![]() in the 2d equation, –1, is the contrary of the coefficient of
in the 2d equation, –1, is the contrary of the coefficient of![]() in the first equation, ane. We can add together the two equations to eliminate
in the first equation, ane. We can add together the two equations to eliminate![]() without needing to multiply by a constant.
without needing to multiply by a constant.
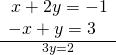
Now that we have eliminated![]() we can solve the resulting equation for
we can solve the resulting equation for![]()
![]()
So, we substitute this value for![]() into one of the original equations and solve for
into one of the original equations and solve for![]()
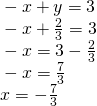
The solution to this arrangement is![]()
Check the solution in the get-go equation.
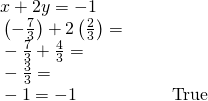 [/hidden-reply]
[/hidden-reply]
Analysis
We gain an of import perspective on systems of equations by looking at the graphical representation. Run into (Figure) to detect that the equations intersect at the solution. We do not need to ask whether in that location may be a second solution because observing the graph confirms that the organization has exactly one solution.
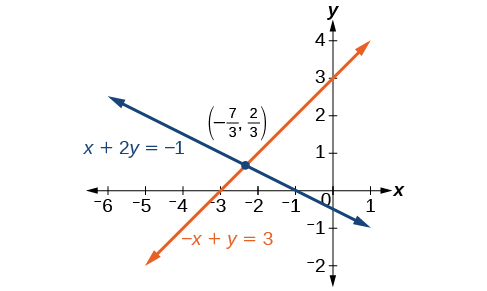
Using the Add-on Method When Multiplication of One Equation Is Required
Solve the given system of equations by the addition method.
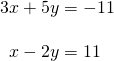
[reveal-answer q="fs-id1165137611459″]Show Solution[/reveal-respond]
[hidden-respond a="fs-id1165137611459″]
Adding these equations as presented will not eliminate a variable. Even so, we see that the get-go equation has![]() in it and the second equation has
in it and the second equation has![]() So if we multiply the 2d equation by
So if we multiply the 2d equation by![]() the x-terms volition add to nil.
the x-terms volition add to nil.

At present, let's add them.
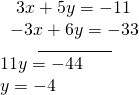
For the last footstep, we substitute![]() into 1 of the original equations and solve for
into 1 of the original equations and solve for![]()
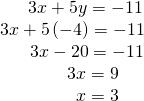
Our solution is the ordered pair![]() See (Figure). Bank check the solution in the original second equation.
See (Figure). Bank check the solution in the original second equation.
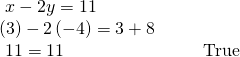
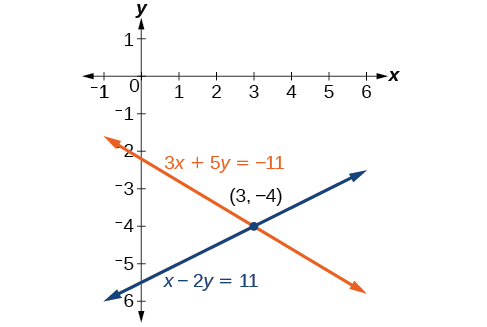
[/subconscious-answer]
Try It
Solve the system of equations by addition.
![]()
[reveal-reply q="fs-id1165137884374″]Show Solution[/reveal-respond]
[hidden-answer a="fs-id1165137884374″]
![]()
[/hidden-respond]
Using the Addition Method When Multiplication of Both Equations Is Required
Solve the given system of equations in two variables by addition.
![]()
[reveal-answer q="fs-id1165134547404″]Prove Solution[/reveal-answer]
[hidden-respond a="fs-id1165134547404″]
Ane equation has![]() and the other has
and the other has![]() The least common multiple is
The least common multiple is![]() so we will take to multiply both equations by a constant in social club to eliminate ane variable. Permit's eliminate
so we will take to multiply both equations by a constant in social club to eliminate ane variable. Permit's eliminate![]() by multiplying the first equation by
by multiplying the first equation by![]() and the 2nd equation by
and the 2nd equation by![]()
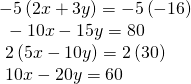
Then, we add the two equations together.
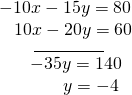
Substitute![]() into the original beginning equation.
into the original beginning equation.
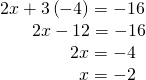
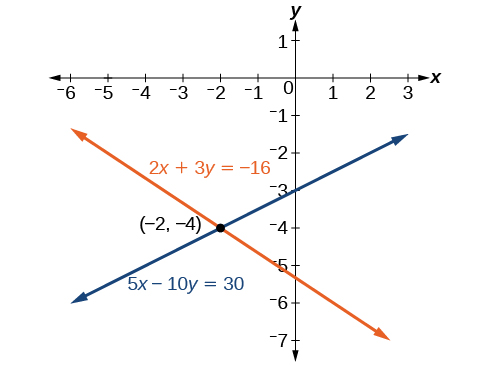
The solution is![]() Check it in the other equation.
Check it in the other equation.
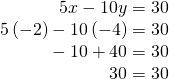
See (Figure).
[/hidden-answer]
Using the Addition Method in Systems of Equations Containing Fractions
Solve the given system of equations in two variables by add-on.
![]()
[reveal-answer q="fs-id1165135154453″]Testify Solution[/reveal-answer]
[hidden-answer a="fs-id1165135154453″]
First articulate each equation of fractions past multiplying both sides of the equation past the to the lowest degree mutual denominator.
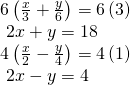
At present multiply the second equation by![]() so that nosotros can eliminate the 10-variable.
so that nosotros can eliminate the 10-variable.
![]()
Add the two equations to eliminate the ten-variable and solve the resulting equation.
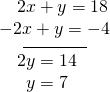
Substitute![]() into the get-go equation.
into the get-go equation.
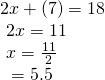
The solution is![]() Bank check information technology in the other equation.
Bank check information technology in the other equation.
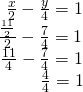 [/subconscious-answer]
[/subconscious-answer]
Endeavor It
Solve the system of equations past improver.
![]()
[reveal-reply q="fs-id1165135547107″]Bear witness Solution[/reveal-respond]
[subconscious-respond a="fs-id1165135547107″]
![]()
[/subconscious-answer]
Identifying Inconsistent Systems of Equations Containing Two Variables
Now that nosotros have several methods for solving systems of equations, we can use the methods to identify inconsistent systems. Recall that an inconsistent system consists of parallel lines that have the same slope simply dissimilar![]() -intercepts. They will never intersect. When searching for a solution to an inconsistent system, nosotros volition come up with a false statement, such as
-intercepts. They will never intersect. When searching for a solution to an inconsistent system, nosotros volition come up with a false statement, such as![]()
Solving an Inconsistent Organization of Equations
Solve the following organization of equations.
![]()
[reveal-answer q="fs-id1165135369110″]Bear witness Solution[/reveal-answer]
[hidden-answer a="fs-id1165135369110″]
We can approach this problem in ii ways. Considering one equation is already solved for![]() the virtually obvious step is to utilise substitution.
the virtually obvious step is to utilise substitution.
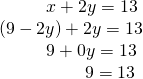
Clearly, this argument is a contradiction considering![]() Therefore, the system has no solution.
Therefore, the system has no solution.
The second approach would be to beginning manipulate the equations so that they are both in slope-intercept grade. We manipulate the commencement equation as follows.
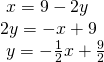
Nosotros then convert the second equation expressed to slope-intercept course.
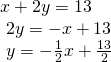
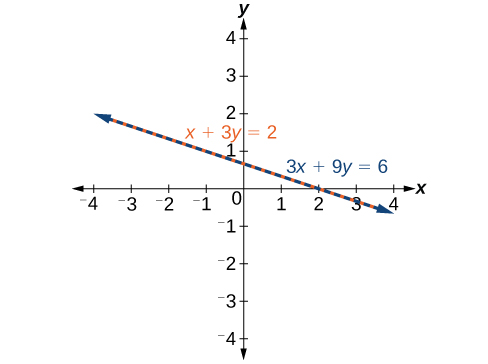
Comparing the equations, we see that they have the same gradient only unlike y-intercepts. Therefore, the lines are parallel and do not intersect.
![]() [/subconscious-answer]
[/subconscious-answer]
Assay
Writing the equations in slope-intercept form confirms that the system is inconsistent considering all lines will intersect eventually unless they are parallel. Parallel lines will never intersect; thus, the ii lines have no points in common. The graphs of the equations in this instance are shown in (Effigy).
Effort It
Solve the following system of equations in two variables.
![]()
[reveal-reply q="fs-id1165135189710″]Evidence Solution[/reveal-answer]
[hidden-reply a="fs-id1165135189710″]
No solution. It is an inconsistent organization.
[/subconscious-answer]
Expressing the Solution of a System of Dependent Equations Containing Ii Variables
Recollect that a dependent system of equations in two variables is a system in which the two equations represent the same line. Dependent systems have an space number of solutions because all of the points on ane line are too on the other line. After using substitution or addition, the resulting equation will be an identity, such equally![]()
Finding a Solution to a Dependent System of Linear Equations
Notice a solution to the system of equations using the addition method.
![]()
[reveal-respond q="fs-id1165134339902″]Bear witness Solution[/reveal-reply]
[hidden-reply a="fs-id1165134339902″]
With the addition method, nosotros want to eliminate one of the variables past adding the equations. In this case, let's focus on eliminating![]() If nosotros multiply both sides of the first equation by
If nosotros multiply both sides of the first equation by![]() then we volition be able to eliminate the
then we volition be able to eliminate the![]() -variable.
-variable.
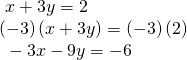
Now add the equations.
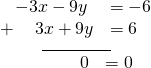
Nosotros tin meet that there will be an space number of solutions that satisfy both equations.
[/hidden-reply]
Analysis
If we rewrote both equations in the slope-intercept form, we might know what the solution would look similar before adding. Let's look at what happens when we catechumen the system to gradient-intercept course.
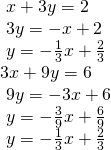
Run into (Figure). Notice the results are the aforementioned. The general solution to the organisation is![]()
Try It
Solve the post-obit arrangement of equations in two variables.
![]()
[reveal-respond q="fs-id1165135176847″]Evidence Solution[/reveal-answer]
[hidden-respond a="fs-id1165135176847″]
The system is dependent so there are infinite solutions of the form![]()
[/subconscious-answer]
Using Systems of Equations to Investigate Profits
Using what we have learned about systems of equations, we can return to the skateboard manufacturing trouble at the kickoff of the section. The skateboard manufacturer'due south acquirement role is the function used to calculate the corporeality of money that comes into the business. It tin be represented by the equation![]() where
where![]() quantity and
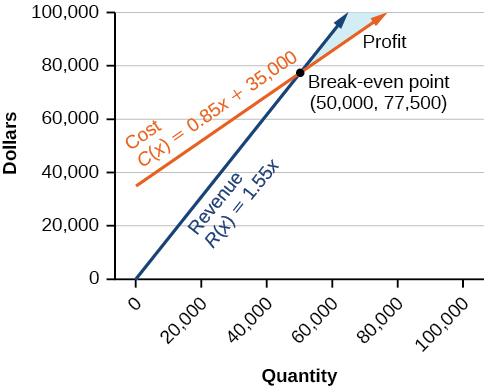
quantity and![]() price. The acquirement function is shown in orange in (Figure).
price. The acquirement function is shown in orange in (Figure).
The cost function is the function used to calculate the costs of doing business. It includes stock-still costs, such as rent and salaries, and variable costs, such as utilities. The toll function is shown in blue in (Effigy). The![]() -axis represents quantity in hundreds of units. The y-centrality represents either cost or revenue in hundreds of dollars.
-axis represents quantity in hundreds of units. The y-centrality represents either cost or revenue in hundreds of dollars.
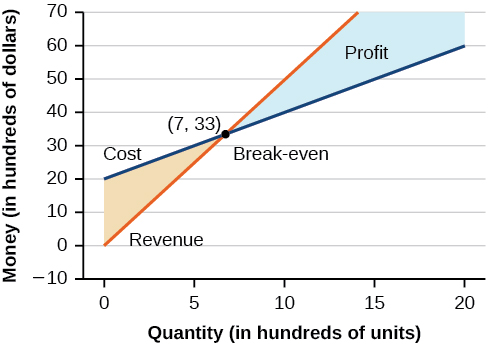
The point at which the ii lines intersect is chosen the break-even indicate. We can come across from the graph that if 700 units are produced, the cost is $3,300 and the revenue is as well $iii,300. In other words, the company breaks even if they produce and sell 700 units. They neither make money nor lose money.
The shaded region to the correct of the break-even point represents quantities for which the company makes a profit. The shaded region to the left represents quantities for which the visitor suffers a loss. The profit role is the acquirement office minus the price office, written equally![]() Clearly, knowing the quantity for which the cost equals the revenue is of keen importance to businesses.
Clearly, knowing the quantity for which the cost equals the revenue is of keen importance to businesses.
Finding the Pause-Fifty-fifty Bespeak and the Turn a profit Function Using Substitution
Given the toll office![]() and the revenue function
and the revenue function![]() discover the intermission-even point and the profit function.
discover the intermission-even point and the profit function.
[reveal-answer q="fs-id1165135417008″]Show Solution[/reveal-answer]
[hidden-answer a="fs-id1165135417008″]
Write the system of equations using![]() to supersede role notation.
to supersede role notation.
![]()
Substitute the expression![]() from the first equation into the 2nd equation and solve for
from the first equation into the 2nd equation and solve for![]()
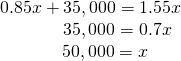
Then, we substitute![]() into either the cost function or the revenue role.
into either the cost function or the revenue role.
![]()
The break-even point is![]()
The profit function is establish using the formula![]()
![]()
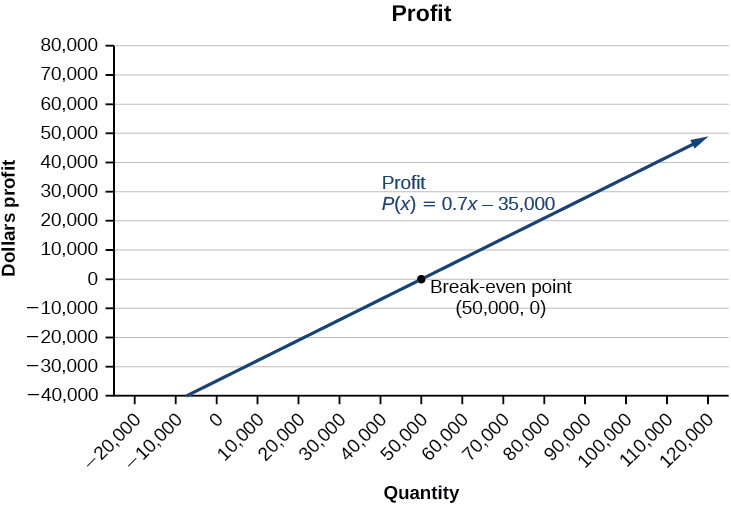
The turn a profit function is![]() [/hidden-answer]
[/hidden-answer]
Analysis
The toll to produce fifty,000 units is $77,500, and the revenue from the sales of l,000 units is besides $77,500. To make a profit, the concern must produce and sell more than fifty,000 units. See (Effigy).
We come across from the graph in (Figure) that the profit function has a negative value until![]() when the graph crosses the x-axis. And then, the graph emerges into positive y-values and continues on this path as the profit function is a direct line. This illustrates that the interruption-even point for businesses occurs when the profit function is 0. The area to the left of the intermission-even betoken represents operating at a loss.
when the graph crosses the x-axis. And then, the graph emerges into positive y-values and continues on this path as the profit function is a direct line. This illustrates that the interruption-even point for businesses occurs when the profit function is 0. The area to the left of the intermission-even betoken represents operating at a loss.
[reveal-answer q="fs-id1165135173070″]Show Solution[/reveal-reply]
[subconscious-answer a="fs-id1165135173070″]
Let c = the number of children and a = the number of adults in attendance.
The total number of people is![]() Nosotros can utilise this to write an equation for the number of people at the circus that twenty-four hours.
Nosotros can utilise this to write an equation for the number of people at the circus that twenty-four hours.
![]()
The revenue from all children tin can exist found by multiplying![]() past the number of children,
past the number of children,![]() The revenue from all adults can be found past multiplying
The revenue from all adults can be found past multiplying![]() by the number of adults,
by the number of adults,![]() The full acquirement is
The full acquirement is![]() We can employ this to write an equation for the revenue.
We can employ this to write an equation for the revenue.
![]()
Nosotros now have a arrangement of linear equations in two variables.
![]()
In the first equation, the coefficient of both variables is 1. We can quickly solve the first equation for either![]() or
or![]() Nosotros will solve for
Nosotros will solve for![]()
![]()
Substitute the expression![]() in the second equation for
in the second equation for![]() and solve for
and solve for![]()
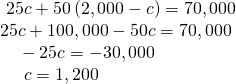
Substitute![]() into the first equation to solve for
into the first equation to solve for![]()
![]()
We find that![]() children and
children and![]() adults bought tickets to the circus that 24-hour interval.[/hidden-answer]
adults bought tickets to the circus that 24-hour interval.[/hidden-answer]
Try It
Meal tickets at the circus toll![]() for children and
for children and![]() for adults. If
for adults. If![]() meal tickets were bought for a total of
meal tickets were bought for a total of![]() how many children and how many adults bought meal tickets?
how many children and how many adults bought meal tickets?
[reveal-answer q="fs-id1165134483375″]Show Solution[/reveal-answer]
[hidden-respond a="fs-id1165134483375″]
700 children, 950 adults
[/subconscious-reply]
Key Concepts
- A system of linear equations consists of two or more equations fabricated up of two or more variables such that all equations in the system are considered simultaneously.
- The solution to a organisation of linear equations in two variables is whatsoever ordered pair that satisfies each equation independently. See (Figure).
- Systems of equations are classified as independent with i solution, dependent with an space number of solutions, or inconsistent with no solution.
- One method of solving a system of linear equations in two variables is by graphing. In this method, nosotros graph the equations on the aforementioned set of axes. Run into (Figure).
- Another method of solving a system of linear equations is past substitution. In this method, we solve for one variable in one equation and substitute the result into the 2nd equation. Come across (Figure).
- A tertiary method of solving a system of linear equations is past improver, in which we can eliminate a variable by adding contrary coefficients of corresponding variables. Encounter (Effigy).
- It is oftentimes necessary to multiply 1 or both equations by a constant to facilitate elimination of a variable when adding the two equations together. See (Figure), (Figure), and (Figure).
- Either method of solving a system of equations results in a false argument for inconsistent systems because they are made up of parallel lines that never intersect. See (Figure).
- The solution to a system of dependent equations will always be true because both equations describe the same line. See (Figure).
- Systems of equations can exist used to solve existent-world problems that involve more than ane variable, such as those relating to acquirement, cost, and profit. See (Figure) and (Figure).
Department Exercises
Verbal
Tin can a organisation of linear equations have exactly ii solutions? Explain why or why not.
[reveal-answer q="fs-id1165133393406″]Show Solution[/reveal-answer]
[hidden-answer a="fs-id1165133393406″]
No, you can either have nil, one, or infinitely many. Examine graphs.
[/hidden-answer]
If you are performing a break-even analysis for a business concern and their cost and revenue equations are dependent, explain what this ways for the company's turn a profit margins.
If y'all are solving a break-even analysis and get a negative break-even point, explicate what this signifies for the company?
[reveal-answer q="fs-id1165133305360″]Show Solution[/reveal-respond]
[subconscious-respond a="fs-id1165133305360″]
This ways there is no realistic break-even point. By the fourth dimension the company produces 1 unit they are already making profit.
[/hidden-answer]
If you are solving a break-even analysis and in that location is no break-even point, explicate what this means for the company. How should they ensure there is a suspension-even point?
Given a system of equations, explicate at least 2 different methods of solving that arrangement.
[reveal-answer q="fs-id1165133305378″]Show Solution[/reveal-answer]
[hidden-answer a="fs-id1165133305378″]
You can solve by substitution (isolating![]() or
or![]() ), graphically, or past improver.
), graphically, or past improver.
[/hidden-answer]
Algebraic
For the following exercises, decide whether the given ordered pair is a solution to the arrangement of equations.
![]() and
and![]()
![]() and
and![]()
[reveal-answer q="fs-id1165135199325″]Show Solution[/reveal-answer]
[hidden-answer a="fs-id1165135199325″]
Yeah
[/hidden-answer]
![]() and
and![]()
![]() and
and![]()
[reveal-respond q="fs-id1165134350004″]Show Solution[/reveal-answer]
[subconscious-answer a="fs-id1165134350004″]
Yep
[/subconscious-answer]
![]() and
and![]()
For the post-obit exercises, solve each organization by substitution.
![]()
[reveal-reply q="fs-id1165135539001″]Show Solution[/reveal-answer]
[hidden-answer a="fs-id1165135539001″]
![]()
[/hidden-reply]
![]()
![]()
[reveal-answer q="fs-id1165134323576″]Show Solution[/reveal-reply]
[subconscious-answer a="fs-id1165134323576″]
![]()
[/hidden-answer]
![]()
![]()
[reveal-respond q="fs-id1165137938420″]Testify Solution[/reveal-answer]
[subconscious-answer a="fs-id1165137938420″]
![]()
[/hidden-respond]
![]()
![]()
[reveal-answer q="fs-id1165133370749″]Show Solution[/reveal-answer]
[hidden-respond a="fs-id1165133370749″]
No solutions be.
[/hidden-answer]
![]()
![]()
[reveal-answer q="fs-id1165134087628″]Bear witness Solution[/reveal-answer]
[hidden-answer a="fs-id1165134087628″]
![]()
[/hidden-answer]
![]()
For the following exercises, solve each system past addition.
![]()
[reveal-reply q="fs-id1165133237152″]Show Solution[/reveal-answer]
[hidden-answer a="fs-id1165133237152″]
![]()
[/hidden-answer]
![]()
![]()
[reveal-answer q="fs-id1165137835514″]Evidence Solution[/reveal-reply]
[hidden-answer a="fs-id1165137835514″]
![]()
[/subconscious-answer]
![]()
![]()
[reveal-answer q="fs-id1165134179654″]Evidence Solution[/reveal-reply]
[subconscious-answer a="fs-id1165134179654″]
No solutions exist.
[/subconscious-answer]
![]()
![]()
[reveal-answer q="fs-id1165134116811″]Show Solution[/reveal-answer]
[hidden-reply a="fs-id1165134116811″]
![]()
[/hidden-answer]
![]()
![]()
[reveal-answer q="fs-id1165132041743″]Prove Solution[/reveal-answer]
[hidden-reply a="fs-id1165132041743″]
![]()
[/hidden-respond]
![]()
For the post-obit exercises, solve each system past any method.
![]()
[reveal-answer q="fs-id1165135397097″]Show Solution[/reveal-respond]
[hidden-answer a="fs-id1165135397097″]
![]() [/hidden-answer]
[/hidden-answer]
![]()
![]()
[reveal-answer q="fs-id1165135586948″]Show Solution[/reveal-answer]
[hidden-answer a="fs-id1165135586948″]
![]()
[/hidden-reply]
![]()
![]()
[reveal-answer q="fs-id1165135555431″]Testify Solution[/reveal-reply]
[hidden-answer a="fs-id1165135555431″]
![]()
[/hidden-answer]
![]()
![]()
[reveal-answer q="fs-id1165134167283″]Show Solution[/reveal-answer]
[hidden-answer a="fs-id1165134167283″]
![]()
[/subconscious-answer]
![]()
![]()
[reveal-reply q="fs-id1165134118216″]Show Solution[/reveal-answer]
[hidden-reply a="fs-id1165134118216″]
![]()
[/hidden-respond]
![]()
Graphical
For the following exercises, graph the arrangement of equations and state whether the system is consistent, inconsistent, or dependent and whether the system has ane solution, no solution, or infinite solutions.
![]()
[reveal-answer q="fs-id1165134279202″]Bear witness Solution[/reveal-answer]
[hidden-answer a="fs-id1165134279202″]
Consistent with ane solution
[/hidden-answer]
![]()
![]()
[reveal-answer q="fs-id1165134475652″]Prove Solution[/reveal-reply]
[hidden-answer a="fs-id1165134475652″]
Consequent with 1 solution
[/hidden-reply]
![]()
![]()
[reveal-respond q="fs-id1165133290327″]Bear witness Solution[/reveal-answer]
[hidden-reply a="fs-id1165133290327″]
Dependent with infinitely many solutions
[/hidden-respond]
Engineering
For the post-obit exercises, apply the intersect part on a graphing device to solve each arrangement. Round all answers to the nearest hundredth.
![]()
![]()
[reveal-answer q="fs-id1165134186354″]Show Solution[/reveal-answer]
[subconscious-answer a="fs-id1165134186354″]
![]()
[/hidden-answer]
![]()
![]()
[reveal-respond q="fs-id1165131880336″]Prove Solution[/reveal-answer]
[hidden-answer a="fs-id1165131880336″]
![]()
[/hidden-answer]
![]()
Extensions
For the post-obit exercises, solve each organization in terms of![]() and
and![]() where
where![]() are nonzero numbers. Note that
are nonzero numbers. Note that![]() and
and![]()
![]()
[reveal-answer q="fs-id1165137832653″]Evidence Solution[/reveal-answer]
[hidden-answer a="fs-id1165137832653″]
![]()
[/hidden-reply]
![]()
![]()
[reveal-reply q="fs-id1165134494238″]Show Solution[/reveal-reply]
[hidden-answer a="fs-id1165134494238″]
![]()
[/hidden-answer]
![]()
![]()
[reveal-answer q="fs-id1165133252901″]Testify Solution[/reveal-answer]
[hidden-answer a="fs-id1165133252901″]
![]()
[/hidden-reply]
Real-World Applications
For the following exercises, solve for the desired quantity.
A stuffed fauna business has a total cost of production![]() and a revenue function
and a revenue function![]() Find the interruption-even point.
Find the interruption-even point.
A fast-food eating house has a cost of production![]() and a revenue part
and a revenue part![]() When does the company offset to turn a profit?
When does the company offset to turn a profit?
[reveal-answer q="fs-id1165133315058″]Show Solution[/reveal-respond]
[hidden-answer a="fs-id1165133315058″]
They never plow a profit.
[/hidden-answer]
A prison cell phone mill has a cost of product![]() and a revenue office
and a revenue office![]() What is the break-even betoken?
What is the break-even betoken?
A musician charges![]() where
where![]() is the full number of attendees at the concert. The venue charges $80 per ticket. After how many people buy tickets does the venue break even, and what is the value of the total tickets sold at that point?
is the full number of attendees at the concert. The venue charges $80 per ticket. After how many people buy tickets does the venue break even, and what is the value of the total tickets sold at that point?
[reveal-answer q="fs-id1165135633718″]Show Solution[/reveal-answer]
[hidden-respond a="fs-id1165135633718″]
![]()
[/hidden-answer]
A guitar factory has a price of product![]() If the visitor needs to interruption even later 150 units sold, at what price should they sell each guitar? Circular upwardly to the nearest dollar, and write the revenue function.
If the visitor needs to interruption even later 150 units sold, at what price should they sell each guitar? Circular upwardly to the nearest dollar, and write the revenue function.
For the following exercises, utilize a arrangement of linear equations with two variables and two equations to solve.
Notice ii numbers whose sum is 28 and difference is 13.
[reveal-answer q="fs-id1165131863016″]Show Solution[/reveal-reply]
[hidden-answer a="fs-id1165131863016″]
The numbers are 7.5 and 20.5.
[/hidden-respond]
A number is 9 more than another number. Twice the sum of the two numbers is 10. Find the ii numbers.
The startup cost for a restaurant is $120,000, and each meal costs $10 for the eating place to make. If each meal is then sold for $15, after how many meals does the eating place break even?
[reveal-answer q="fs-id1165134199409″]Evidence Solution[/reveal-answer]
[subconscious-respond a="fs-id1165134199409″]
24,000
[/hidden-answer]
A moving company charges a flat rate of $150, and an additional $5 for each box. If a taxi service would charge $20 for each box, how many boxes would you need for information technology to be cheaper to use the moving visitor, and what would exist the total toll?
A total of one,595 first- and second-twelvemonth higher students gathered at a pep rally. The number of freshmen exceeded the number of sophomores by fifteen. How many freshmen and sophomores were in attendance?
[reveal-reply q="fs-id1165134199428″]Show Solution[/reveal-respond]
[hidden-reply a="fs-id1165134199428″]
790 sophomores, 805 freshman
[/hidden-answer]
276 students enrolled in a freshman-level chemistry class. By the end of the semester, 5 times the number of students passed as failed. Find the number of students who passed, and the number of students who failed.
In that location were 130 faculty at a conference. If there were 18 more than women than men attending, how many of each gender attended the briefing?
[reveal-answer q="fs-id1165134254374″]Show Solution[/reveal-answer]
[hidden-answer a="fs-id1165134254374″]
56 men, 74 women
[/subconscious-answer]
A jeep and BMW enter a highway running east-west at the same leave heading in opposite directions. The jeep entered the highway 30 minutes before the BMW did, and traveled 7 mph slower than the BMW. After 2 hours from the fourth dimension the BMW entered the highway, the cars were 306.5 miles autonomously. Find the speed of each machine, assuming they were driven on cruise control.
If a scientist mixed 10% saline solution with 60% saline solution to get 25 gallons of 40% saline solution, how many
gallons of 10% and sixty% solutions were mixed?
[reveal-respond q="fs-id1165134254393″]Testify Solution[/reveal-respond]
[hidden-answer a="fs-id1165134254393″]
10 gallons of ten% solution, xv gallons of threescore% solution
[/hidden-reply]
An investor earned triple the profits of what she earned last year. If she fabricated $500,000.48 total for both years, how much did she earn in profits each yr?
An investor who dabbles in real estate invested one.one million dollars into two land investments. On the kickoff investment, Swan Peak, her return was a 110% increase on the money she invested. On the 2d investment, Riverside Community, she earned fifty% over what she invested. If she earned $1 million in profits, how much did she invest in each of the land deals?
[reveal-answer q="fs-id1165133227646″]Show Solution[/reveal-answer]
[subconscious-reply a="fs-id1165133227646″]
Swan Peak: $750,000, Riverside: $350,000
[/subconscious-respond]
If an investor invests a total of $25,000 into two bonds, one that pays 3% simple interest, and the other that pays
*** QuickLaTeX cannot compile formula: \,2\frac{seven}{8}\text{%}\, *** Fault bulletin: File concluded while scanning use of \text@. Emergency stop. interest, and the investor earns $737.l annual interest, how much was invested in each account?
If an investor invests $23,000 into two bonds, one that pays 4% in simple involvement, and the other paying 2% simple interest, and the investor earns $710.00 annual involvement, how much was invested in each account?
[reveal-answer q="fs-id1165134061799″]Show Solution[/reveal-respond]
[hidden-respond a="fs-id1165134061799″]
$12,500 in the first business relationship, $10,500 in the second account.
[/hidden-answer]
CDs cost $v.96 more than DVDs at All Bets Are Off Electronics. How much would 6 CDs and two DVDs cost if v CDs and ii DVDs cost $127.73?
A store clerk sold 60 pairs of sneakers. The high-tops sold for $98.99 and the low-tops sold for $129.99. If the receipts for the 2 types of sales totaled $6,404.40, how many of each type of sneaker were sold?
[reveal-answer q="fs-id1165134061817″]Show Solution[/reveal-answer]
[hidden-reply a="fs-id1165134061817″]
High-tops: 45, Low-tops: 15
[/subconscious-answer]
A concert director counted 350 ticket receipts the day after a concert. The price for a student ticket was $12.50, and the toll for an adult ticket was $16.00. The register confirms that $5,075 was taken in. How many student tickets and developed tickets were sold?
Access into an amusement park for four children and 2 adults is $116.ninety. For 6 children and iii adults, the access is $175.35. Assuming a different price for children and adults, what is the cost of the kid'south ticket and the price of the adult ticket?
[reveal-answer q="fs-id1165135363419″]Show Solution[/reveal-reply]
[subconscious-reply a="fs-id1165135363419″]
Infinitely many solutions. We demand more information.
[/hidden-answer]
Source: https://opentextbc.ca/algebratrigonometryopenstax/chapter/systems-of-linear-equations-two-variables/
Post a Comment for "what is the greatest possible number of solutions to the following system of equations? 1 2 3 4"